황금비가 남용되는 이유(1/2)
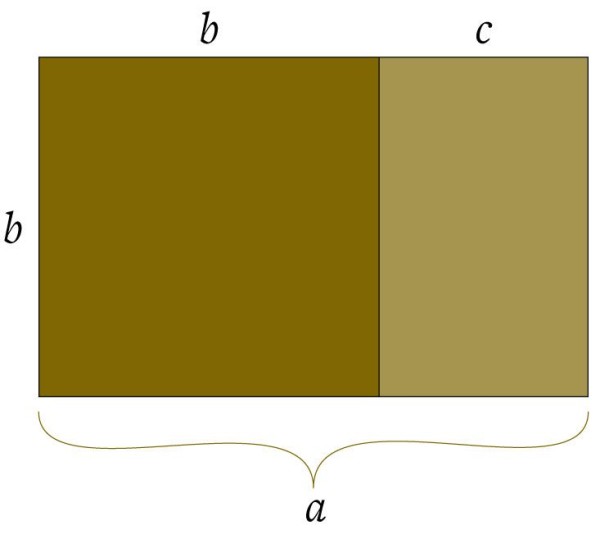
세상에는 수많은 상수가 있지만, 가장 특별한 상수만이 그리스 문자를 할당받고 있습니다. 황금비 파이(φ) 역시 그들 중의 하나입니다. 1.618.. 로 이어지는 이 수는 이상적인 비율의 상징입니다. 어떤 직선 a를 두 부분 b와 c로 나눈다고 해봅시다. 황금비는 a와 b의 비율이 b와 c의 비율과 같을 때 b와 c(곧 a와 b) 사이의 비율을 가리킵니다. 또한, 두 변의 길이 비율이 황금비일 때, 그 직사각형을 황금비 직사각형이라고 부르며, 5각형과 플라톤의 다섯 정다면체들에도 등장합니다. 그리고 앞의 두 수를 더한 수가 다음 수가 되는 수열인 피보나찌 수열에서 연속된 두 수의 비율도 점점 더 황금비에 가까워짐을 알 수 있습니다.
즉, 황금비는 마치 프랙탈이라는 개념과 비슷하게 서로 다른 수학 분야들을 하나로 이어주는 역할을 합니다. 자연 속에서도 황금비는 관찰됩니다. 예를 들어, 양자 수준에서는 자기장을 띈 원자가 황금비로 설명 가능한 에너지 밴드 사이를 진동합니다. 식물의 씨앗과 잎의 형태에서도 피보나찌 수열과 황금비는 등장합니다. 해바라기 꽃에 씨앗들은 시계방향과 반시계방향의 나선이 있으며 이는 피보나찌 수열로 설명할 수 있습니다. 이 배열은 매우 엄격해서, 한 쪽 방향으로는 233개의 씨앗이, 다른 방향으로는 144개의 씨앗이 있습니다. (이 두 수의 비는 황금비입니다) 게다가 황금비를 각도로 변환했을 때의 각인 약 137.5도 역시 해바라기와 줄기에 붙은 나뭇잎에서 관찰됩니다. 마리오 리비오는 자신의 책 “황금비(The Golden Ratio)”에서 황금비가 가장 효율적으로 물건을 쌓는 방식이라고 말합니다. 황금비는 때로 “가장 무리한 수(the most irrational number)”로 불립니다. 이는 황금비가 정수의 비로 나타내기 가장 어려운 수라는 뜻입니다. 따라서 나뭇잎이 황금비의 각도로 가지에서 자라날 경우, 어떤 나뭇잎도 일렬로 상대를 가리지 않게 됩니다.
황금비는 미학과도 관련이 있습니다. 수 세기 동안 어떤 이들은 두 변의 길이가 황금비인 사각형을 가장 아름답다고 주장했습니다. 살바도르 달리와 르 꼬르뷔지에는 황금비를 자신의 작품 속에 녹여 넣었습니다. 달리의 최후의 만찬은 황금비 사각형 캔버스 위에 그려졌으며 예수와 그의 제자들이 찌그러진 12면체 안에 위치하고 있습니다. 르 꼬르뷔지에는 황금비와 인체에 기반을 둔 모듈러(Modulor)라는 측정 방법을 이용해 자신의 건축물을 설계했습니다.
그러나 황금비가 잘못 언급되는 경우도 많습니다. 앵무조개(Nautilus) 껍데기의 나선형이 크기에 상관없이 황금비 사각형 안에 들어간다는 것은 사실이 아닙니다. 앵무조개의 껍데기는 성장하는 동안 계속 같은 모양을 유지하며, 이는 로그 나선(logarithmic spiral)이라는 특성 때문입니다. 그러나 이 비율은 황금비가 아닙니다. 인체의 비율에 황금비가 있다고 주장하는 사람도 있습니다. 구텐베르크 성경 모양에 황금비가 있다거나, 모나리자와 파르테논에도 황금비가 발견된다고 주장합니다. 그러나 이런 주장들은 검증된 적이 없습니다. 수학자 키스 데블린은 황금비에 관한 강연 중 이런 주장들이 거짓임을 보였지만, 정작 이 부분은 방송에서 편집되어 버렸습니다. 왜 사람들은 그렇게 황금비에 관한 이야기를 좋아하는 것일까요?
물론 황금비의 중요성이 과장되고 있는 것은 사실이지만, 주변의 여러 상황에서 이 숫자는 발견되며 수학의 놀라운 힘을 보여줍니다. 행성의 궤도를 설명하는 타원 공식에서 중력을 설명하는 역제곱법칙, 그리고 일상의 에너지 상당수를 설명하는 물리학 법칙인 디랙 공식에 이르기까지 수학은 우주의 구조를 논리적으로 우리에게 설명해줍니다. 사실 우리가 아는 한, 우주는 이런 수학적 법칙에 따라 지배될 필요가 없음에도 불구하고, 지배되고 있는 것입니다. 물리학자 유진 위그너는 이 주제에 관한 논문의 제목을 이렇게 쓴 바 있습니다. “자연과학에 있어서 수학의 이해 불가능할 정도로 놀라운 효율성(The Unreasonable Effectiveness of Mathematics in the Natural Sciences).”
(노틸러스)